Puzzles

Info

• Download data (and answers 😊)

wget -c puzzles_da.tar.gz https://github.com/GenomicsAotearoa/shell-for-bioinformatics/releases/download/v2.0/puzzles_da.tar.gz -O - | tar -xz

• Review the content of the puzzles_da directory

  • There are two directories, data and answers
  • Each filename has a unique four character id which corresponds to the puzzle/question (Described below)

• We recommend appending the solution to a file and compare the content of it with the expected output in answers directory

• How to compare your solution with the provided solution ( introducing two new commands cmp and printf)

#!/bin/bash

if cmp --silent -- "provided_answer.txt" "my_answer.txt"; then
    printf "\U1F60A SUCCESS \n"
else 
    printf "\U1F97A Almost there...Try again please\n" 
fi

• cmp compare two files
• --silent Output nothing; yield exit status only.
• printf format and print data
• if else fi are control statements. This will be covered in depth during the *Advanced shell for Bioinformatics" workshop

Few additional bash commands to help with puzzles

1. tr - translating or deleting characters. It supports a range of transformations including uppercase to lowercase, squeezing repeating characters, deleting specific characters, and basic find and replace. It can be used with UNIX pipes to support more complex translation
   • Let's say we want to replace upper case B in AABBCC ( standard_input) with lower case b, we can use standard_input | tr B b
2. rev - reverse the lines characterwise. This utility basically reverses the order of the characters in each line by copying the specified files to the standard output. If no files are specified, then the standard input will read
   • Suppose the standard input is "Humpty Dumpty sat on a wall", rev standard_input will print "llaw a no tas ytpmuD ytpmuH"

Transcribing DNA into RNA (tdir)

An RNA string is a string formed from the alphabet containing 'A', 'C', 'G', and 'U'.

Given a DNA string \(t\) corresponding to a coding strand, its transcribed RNA string \(u\) is formed by replacing all occurrences of 'T' in \(t\) with 'U' in \(u\)

Given: A DNA string \(t\) having length at most 1000 nt.

Return: The transcribed RNA string of \(t\)

Solution

bashRPythonJuliaC++

There are multiple ways to do this

sed 's/T/U/g' tdir_data.txt

awk '{gsub(/T/,"U");print}' tdir_data.txt

cat tdir_data.txt | tr T U

gsub("T","U",readLines("tdir_data.txt"))

with open('tdir_data.txt', 'r') as f1:
        dna = f1.read()
        rna = dna.replace("T", "U")
        print(rna)

seq = open("tdir_data.txt") do file
    read(file, String)
end

seq = replace(seq, "T" => "U")
println(seq)

// to compile, save the code to tdir.cpp:
// g++ tdir.cpp -o tdir_cpp
// to run:
// cat tdir_data.txt | tdir_cpp > answer

#include <iostream>
using namespace std;            

int main()
{
    char nucleotide;            

    while (cin >>nucleotide) {
        if (nucleotide == 'T') cout <<'U';
        else cout <<nucleotide;
    }
    return 0;
}

---

Complementing a Strand of DNA (csod)

In DNA strings, symbols 'A' and 'T' are complements of each other, as are 'C' and 'G'.

The reverse complement of a DNA string \(s\) is the string \(s^{c}\) formed by reversing the symbols of \(s\) then taking the complement of each symbol (e.g., the reverse complement of "GTCA" is "TGAC").

Given: A DNA string s of length at most 1000 bp.

Return: The reverse complement \(s^{c}\) of \(s\).

Solution

bashPythonJuliaPerlC++

There are multiple ways to do this

rev csod_data.txt | tr ATCG TAGC

rev csod_data.txt | sed 'y/ATCG/TAGC/'

cat csod_data.txt | tr 'ACGT' 'TGCA' | rev

• For multi-line sequences

  tr -d "\n" < data.txt| rev  | tr ATCG TAGC
  

• For FASTA files

  grep -v "^>" r.fasta | tr -d "\n"  | rev  | tr ATCG TAGC
  

for N in open("csod_data.txt","r").read()[::-1]:
    for pair in ["GC","AT"]:
        if N in pair: print("".join(set(N)^set(pair)),end="")

f = read(open("csod_data.txt"), String)

dict = Dict("A"=>"T", "C"=>"G", "T"=>"A", "G"=>"C")

for i in reverse(f[1:end-1])
    print(dict[string(i)])
end

println()

$filename = 'csod_data.txt';
open(FILEN, $filename);            

$dna = <FILEN>;            

$rev = reverse $dna;
$rev =~ tr/ATCG/TAGC/;            

print $rev;            

exit;

// to compile, save the code as csod.cpp
// g++ csod.cpp -o csod_cpp
// to run:
// cat csod_data.txt | ./csod_cpp > answer

#include <iostream>
#include <vector>            

char complement(const char c)
{
    switch(c) {
        case 'A': return 'T';
        case 'T': return 'A';
        case 'C': return 'G';
        case 'G': return 'C';
    }
    return 'X';
}            

int main()
{
    using std::cin;
    using std::cout;
    using std::vector;            

    char nucleotide;
    vector<char> DNAstring;            

    while (cin >>nucleotide) {
        DNAstring.push_back(nucleotide);
    }
    for (int pos = DNAstring.size()-1; pos >= 0; --pos) {
        cout <<complement(DNAstring[pos]);
    }            

    return 0;
}

---

Counting DNA Nucleotides (dnct)

A string is simply an ordered collection of symbols selected from some alphabet and formed into a word; the length of a string is the number of symbols that it contains.

An example of a length 21 DNA string (whose alphabet contains the symbols 'A', 'C', 'G', and 'T') is "ATGCTTCAGAAAGGTCTTACG."

Given: A DNA string \(s\) of length at most 1000 nt.

Return: Four integers (separated by spaces) counting the respective number of times that the symbols 'A', 'C', 'G', and 'T' occur in \(s\)

Solution

bashPythonRust

awk '{a=gsub("A","");c=gsub("C","");g=gsub("G","");t=gsub("T","")} END {print a,c,g,t}' /path/to/file x=$(cat dnct_data.txt); for i in A C G T; do y=${x//[^$i]}; echo -n "${#y} "; done

• A bit more simpler solution in bash

  for i in A C G T;do grep -o $i dnct_data.txt | wc -l; done
  

with open('dnct_data.txt') as file:
    dataset = file.read()

print(dataset.count('A'), dataset.count('C'), dataset.count('G'), dataset.count('T'))

// to compile, save the code as dnct.rs
// rustc dnct.rs            

use std::fs::File;
use std::io::{Read, Write};            

fn dna_parse(in_str: &str) -> (i32, i32, i32, i32) {
    let mut a_count = 0;
    let mut c_count = 0;
    let mut g_count = 0;
    let mut t_count = 0;
    for symbol in in_str.chars() {
        match symbol {
            'A' | 'a' => a_count += 1,
            'C' | 'c' => c_count += 1,
            'G' | 'g' => g_count += 1,
            'T' | 't' => t_count += 1,
            '\r' | '\n' => (),
            x => println!("Unknown DNA symbol: {}", x.escape_debug())
        };
    }
    (a_count, c_count, g_count, t_count)
}            

fn main() -> std::io::Result<()> {
    // Get the input data
    let mut in_file = File::open("dnct_data.txt")?;
    let mut contents = String::new();
    in_file.read_to_string(&mut contents)?;            

    // Process the data
    let (a, c, g, t) = dna_parse(&contents);
    let out_str = format!("{} {} {} {}", a, c, g, t);            

    // Export the data
    let mut out_file = File::create("dnct_answer.txt")?;
    out_file.write_all(out_str.as_bytes())?;
    Ok(())
}

---

Maximum Matchings and RNA Secondary Structures (mmrs)

Figure

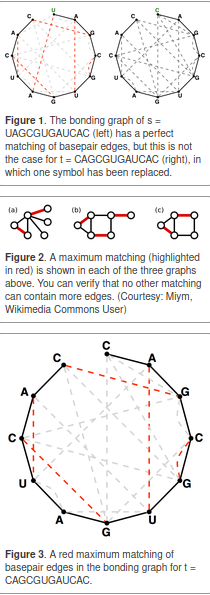
The graph theoretical analogue of the quandary stated in the introduction above is that if we have an RNA string \(s\) that does not have the same number of occurrences of 'C' as 'G' and the same number of occurrences of 'A' as 'U', then the bonding graph of \(s\) cannot possibly possess a perfect matching among its basepair edges. For example, see Figure 1; in fact, most bonding graphs will not contain a perfect matching.

In light of this fact, we define a maximum matching in a graph as a matching containing as many edges as possible. See Figure 2 for three maximum matchings in graphs.

A maximum matching of basepair edges will correspond to a way of forming as many base pairs as possible in an RNA string, as shown in Figure 3.

Given: An RNA string \(s\) of length at most 100.

Return: The total possible number of maximum matchings of basepair edges in the bonding graph of \(s\)

Solution

bashPython

#!/bin/bash

dna="$(cat mmrs_data.txt | tail -n +2 | tr -d '\n')"

count () {
    echo -n "${dna//[^$1]/}" | wc -c
}

matches () {
local n1=$(count $1)
local n2=$(count $2)
if test $n2 -gt $n1; then
    local tmp=$n1
    n1=$n2
    n2=$tmp
fi
seq -s \* $((n1 - n2 + 1)) $n1
}

echo "$(matches A U) * $(matches C G)" | bc 

from Bio import SeqIO
from scipy.special import perm

with open('mmrs_data.txt', encoding='utf-8') as handle:
    rna = SeqIO.read(handle, 'fasta').seq

au, cg = (rna.count('A'), rna.count('U')), (rna.count('C'), rna.count('G'))
print(perm(max(au), min(au), exact=True) * perm(max(cg), min(cg), exact=True))

---

Computing GC Content (cgcc)

The GC-content of a DNA string is given by the percentage of symbols in the string that are 'C' or 'G'. For example, the GC-content of "AGCTATAG" is 37.5%. Note that the reverse complement of any DNA string has the same GC-content.

DNA strings must be labeled when they are consolidated into a database. A commonly used method of string labeling is called FASTA format. In this format, the string is introduced by a line that begins with '>', followed by some labeling information. Subsequent lines contain the string itself; the first line to begin with '>' indicates the label of the next string.

In our implementation, a string in FASTA format will be labeled by the ID "GAotearoa_xxxx", where "xxxx" denotes a four-digit code between 0000 and 9999.

Given: At most 10 DNA strings in FASTA format (of length at most 1 kbp each).

Return: The ID of the string having the highest GC-content, followed by the GC-content of that string. Rosalind allows for a default error of 0.001 in all decimal answers unless otherwise stated; please see the note on absolute error below.

Solution

bashPerlR (with seqinr)PythonPython (🤓 version)

#/bin/bash

awk -v RS=">" -v FS="\n" 'BEGIN {max_id=""; max_gc="";} \
$0 !="" { \
gc=0; \
l=0; \
for(i=2;i<=NF;i++) { \
    gc += gsub(/[GC]/, ".", $i); \
    l += length($i);} \
    if(max_gc < gc/l*100) {max_id=$1; max_gc=gc/l*100} \
} \
END {print max_id"\n"max_gc;}' cgcc_data.txt

perl -ne 'BEGIN{$/="\n>";$gc=-1}chomp;s/^>//;($id,$seq)=(split(/\n/,$_,2));$seq=~s/\n//g;$cgc=100*(($seq=~y/GC//)/length($seq));if($cgc>$gc){$gc=$cgc;$gcid=$id};END{print "$gcid\n$gc\n"}' data/cgcc_data.txt

library(seqinr)
fasta <- read.fasta("cgcc_data.txt")
gc_content <- apply(matrix(names(fasta)), 1, function(x){GC(fasta[[x]])})
most_gc <- which(gc_content==max(gc_content))

#Result
rbind(names(fasta)[most_gc], paste(signif(gc_content[most_gc], 4) * 100, "%", sep=""))

from Bio import SeqIO
from Bio.Seq import Seq
from Bio.Alphabet import IUPAC
from Bio.SeqUtils import GC
max_seq = Seq('tata', IUPAC.unambiguous_dna)
max_gc = ()
for seq_record in SeqIO.parse('cgcc_data.txt','fasta'):
    if GC(seq_record.seq) > GC(max_seq):
        max_id = seq_record.id
        max_seq = seq_record.seq
        max_gc = GC(seq_record.seq)
print(max_id)
print (max_gc)

from Bio import SeqIO
from Bio.SeqUtils import GC

input_file = 'cgcc_data.txt'
seq_dict = {
    seq_record.id: GC(seq_record.seq)
    for seq_record in SeqIO.parse(input_file, "fasta")
}

max_gc = max(seq_dict, key=seq_dict.get) # find key of the dicionary's max value
print(max_gc)
print(seq_dict[max_gc])

---

Counting Disease Carriers (cdcr)

To model the Hardy-Weinberg principle, assume that we have a population of \(N\) diploid individuals. If an allele is in genetic equilibrium, then because mating is random, we may view the 2\(N\) chromosomes as receiving their alleles uniformly. In other words, if there are m dominant alleles, then the probability of a selected chromosome exhibiting the dominant allele is simply \(p=m/2N\)

Because the first assumption of genetic equilibrium states that the population is so large as to be ignored, we will assume that \(N\) is infinite, so that we only need to concern ourselves with the value of \(p\)

Given: An array \(A\) for which \(A[k]\) represents the proportion of homozygous recessive individuals for the \(k\)-th Mendelian factor in a diploid population. Assume that the population is in genetic equilibrium for all factors.

Return: An array \(B\) having the same length as \(A\) in which \(B[k]\) represents the probability that a randomly selected individual carries at least one copy of the recessive allele for the \(k\)-th factor.

Solution

bash

cat cdcr_data.txt | tr \  '\n' | sed 's/.*/2 * sqrt(&) - &/' | bc -l